Accuracy Precision r 7
Introduction
Observations are vitally important to
all of science. Some observations are qualitative in nature -
such as a change in color of a material, the formation of a gas, or
the formation of solid in a liquid mixture. Many observations,
though, are quantitative. You may measure how much something
weighs, how much product is produced in a chemical reaction, the
distance between two towns, etc. These quantitative observations -
measurements - are done by comparing the thing being measured
to some standard of measurement. This comparison introduces
error, and it is for this reason that we must be careful when
dealing with measurements.
Measurements and units
All measurements are reported with
units , which are
fixed standards of measurement. Any quantitative measurement
should be given with its associated unit. It's one thing to say
Columbia, SC, is 82 miles from Florence, SC, but it's quite
another to say that Florence is 82 inches away from Columbia.
If I tell you Columbia is "82" away from here, you don't
necessarily know what I mean. You'd probably guess miles
- unless you were European and assumed I meant kilometers .
Accuracy and precision
There are two things to worry about
when making a measurement: the accuracy of the measurement and
the precision of the measurement.
The accuracy of a measurement is
the closeness of the measurement to the true value of the
thing being measured. In other words - is the measurement right?
You can check accuracy be measuring a standard - an object
where the measured property has a known value. To check the accuracy
for a scale, for example, you would measure a standard mass on
the scale. If the scale measures a known mass correctly, it probably
measures an unknown mass correctly.
The precision of a measurement
is the reproducibility of the measurement. In other words,
can you measure the same thing multiple times and get the same
result? To check the precision of a measurement, we make multiple
measurements.
How do real-world measurements rate
when it comes to accuracy and precision? There are three common
cases, which we will illustrate using a dart board.
|

|
Measurements (darts) are shown by asterisks "*"
on the dart board.
The true value of the measurement is represented by the
bullseye at the center of the dart board.
In this case, measurements are scattered far apart and not
anywhere near the true value.
|
|
Illustration 1: Neither precise nor accurate
|
|
In the case in Illustration 1, darts
are scattered all over the dart board and nowhere near the bullseye.
Obviously, the person throwing the darts is either a very poor shot
or very drunk! In a lab, this would be a poor set of measurements
done by an inexperienced or lazy experimenter. These measurements
are neither accurate nor precise, and these measurements are
worthless for providing evidence for a hypothesis.
|
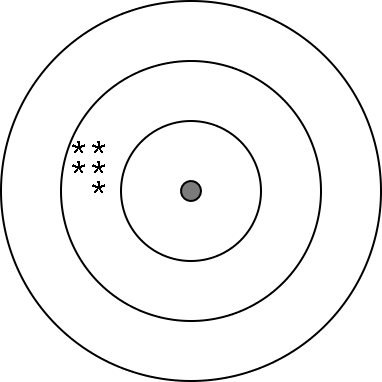
|
In this case, our measurements are reproducible - they all
have approximately the same value.
The measurements, though, are not near the true value.
|
|
Illustration 2: Precise but not accurate.
|
|
In the case shown in Illustration 2,
the measurements have approximately the same value, but are
substantially "off" from the true value. These
measurements are precise but not accurate. These measurements
are not good evidence for a hypothesis. This case is most often
caused by faulty or uncalibrated measuring devices. It is usually
corrected by checking your measuring devices every once in a while
using a known standard and calibrating when necessary.
|

|
In this case, our measurements are reproducible - they all
have approximately the same value.
The measurements are all near the true value.
|
|
Illustration 3: Accurate and precise
|
|
The case shown in illustration 3 is the
best case - the measurements are all nearly the same and they
are all approximately equal to the true value. These measurements
are accurate and precise and are the kind of good data you
need to back up a hypothesis.
Precision and the concept of
significant figures
Since reproducibility (precision) is so
important when taking scientific measurements, we write our
measurements in a way that indicates their precision - using a
convention known as significant figures. To explain what
significant figures are, we'll look at an example.
|

|
Like most laboratory glassware, graduated cylinders come
in a wide variety of sizes.
The yellow plastic ring on the first cylinder and the
white plastic ring on the cylinder third from the left are used
to help read the scale.
|
|
Illustration 4 - Some graduated cylinders
|
|
Graduated cylinders are common
pieces of laboratory glassware. You can use them to measure out
volumes of a liquid. You read a graduated cylinder by looking for
the meniscus (the bottom of the curved surface of water) and
comparing it to the scale on the cylinder.
Let's say that you were trying to read
a graduated cylinder to the best of your ability. Try to read the
cylinder drawn in illustration 5 below:
|

|
You may assume this cylinder is scaled such that each line
represents one milliliter.
Read from the meniscus.
Read to one decimal place better than the scale - make
an estimate of where the bottom surface of the water is
located.
|
|
Illustration 5 - A graduated cylinder containing liquid
|
|
When reading this cylinder, you might
come up with one of several answers: 15.3 mL, 15.5 mL, 15.6
mL, 15.4 mL, or 15.7 mL. It depends on how you estimate the bottom
of the liquid. Some features all these numbers have in common is
that you're certain that the cylinder contains 15 point
something milliliters of liquid. There is some uncertainty in
the last digit, since we estimated
it.
Let's
say that you read the cylinder as 15.4 mL. You would report the
measurement as 15.4 mL. This number actually tells someone else how
precisely you measured the volume. You know the first two digits in
the number with certainty, while the last digit is your estimate (or
"best guess") of how many tenths of a milliliter are in the
cylinder. Significant figures are the certain
digits in a measurement (the
"15" in our example) plus one uncertain digit
(the "4") . We
say that a measurement of 15.4 mL contains "three significant
figures".
It's easy to get the correct number of
significant figures for a measurement:
For measurements where you read
the markings on a scale, the markings indicate your certain digits,
while your uncertain digit is one decimal place better than your
markings.
For most measurements using
digital readouts, take all the digits the measuring device gives.
This is less true for non-scientific equipment like cheap digital
thermometers available in department stores.
For all measurements, you may make
several measurements and find the standard deviation of the
measurements. The standard deviation represents the uncertainty in
a set of measurements. You will do this in one of your first
laboratory experiments.
We have highly precise analytical
balances in our lab to measure mass. If the balance reads 0.2442
g, that's how you would record the measurement. You might notice
that the last digit on these balances may fluctuate slightly. The
balance continually re-estimates the mass of an object on the
balance, so you will sometimes see fluctuations.
|

|
Analytical balances are high-precision mass measurement
devices.
The pan of an analytical balance (where you put the
sample) is enclosed in a glass "cage" to keep air
currents from pushing down the balance and causing errors in the
mass measurement!
Most modern analytical balances (like this one) are
computerized.
Never put chemicals directly on the balance pan! Use a
piece of weighing paper or a weighing boat to keep
chemicals from coming into contact with the pan and damaging it.
|
|
Illustration 6: An analytical balance
|
|
Math with significant figures
So how many significant figures do you
report if you take multiple measurements (each with their own
number of significant figures) and add / subtract / multiply / divide
them? How can you tell how many significant figures are in a
measurement if you didn't do it yourself?
Here are some rules of thumb for
telling what digits are significant in the first place:
Any nonzero digit is
significant.
Zeros at the end of a
number are not considered significant unless there is a
decimal point in the number. The zero in "5.0 cm" is
significant - it means that the length was measured to a tench of a
centimeter. The zeros is "500 miles" aren't significant
unless we're told otherwise. Did the experimenter measure to the
nearest hundred miles, ten miles, or single mile?
Zeros at the beginning of a
number (before any nonzero digit) are not significant. The zero in
"0.42 grams" is in front of the decimal and is put there
simply to make the decimal easier to see. It is not significant.
The three zeros in 0.0038 km are not significant, either.
If a measurement is written in
scientific notation , all
the digits in the mantissa are significant. For example, there are
three significant digits in the measurement "5.00x10 2 "
miles - the one and the two zeros after the decimal point..
Non-significant zeros in a number are
usually called placeholders
- they exist to either show how big or small a number is, or to make
the number easier to read. They are not part of the actual
measurement.
Let's look at a few examples
Significant digits will be underlined:
|
Measurement
|
Number of significant figures
|
Explanation
|
|
0.00420 cm
|
3
|
The three beginning zeros aren't significant - they're
placeholders. The end zero is not a placeholder and is
significant.
|
|
123.456 miles
|
6
|
All nonzero digits are significant.
|
|
102.0 seoonde
|
4
|
The first zero is significant - it was measured. The end zero
is after a decimal - it is not a placeholder.
|
|
500 miles
|
1
|
Unless we're told otherwise, 500 miles must have been measured
to the nearest hundred miles. The zeros are considered
placeholders.
|
|
0.1200 g
|
4
|
The zero in front of the decimal is just a placeholder - it
makes the number easier to read by letting you know a decimal
point is coming up.
|
|
1.230x10-6 kg
|
4
|
The number is in scientific notation.
|
|
12.011 g/mol
|
5
|
The zero is between nonzero digits - it must have been
measured.
|
|
10200 mL
|
3
|
The first zero is between two significant figures (so it was
measured), while two end zeros are placeholders.
|
When doing math with measurements, you
can follow two simple rules (derived from statistics) for math
operations:
When you multiply and divide
measurements, your answer has the same number of significant
figures as the measurement with the least number of significant
figures. In other words, your answer is only as good as your
least precise measurement!
When you add and subtract
measurements, your answer has the same number of decimal
places as the measurement with the least number of decimal places.
Let's look at a few examples:
What is the area of a rectangle with
a length of 54.36 m and a width of 3.57 m?
The area of a rectangle is equal to
length times width, so

The answer above was found by simply
punching the numbers into a calculator. Calculators, though, don't
understand the concept of significant figures and don't know that the
numbers you're punching in come from measurement. We know,
though, that we really don't know the area as precisely as 194.0652
m2, since we got the area by multiplying two length
measurements that contained some degree of uncertainty. The proper
way to report the answer is to use the multiplication / division
rule. Note that 54.26 m has four significant figures while 3.57 m
has three, so the final answer should have three significant
figures.

The
area, rounded to the correct number of significant figures, is 194
m 2 .
Let's try another example.
A quantity of sodium chloride is
weighed in a beaker. The total weight of sodium chloride and beaker
is 164.037 g, while the beaker alone weighs 15.6423 g. What is the
weight of the sodium chloride?
This is a simple subtraction. Subtract
the weight of the beaker from the total weight:
164.037 g - 15.6423 g =
148.3947 g sodium chloride
Again, the answer above was read
straight off a calculator display. We know, though, that we don't
know the weight of the sodium chloride to the precision indicated
above because our total mass measurement's uncertain digit was in the
thousandths place. If that digit is uncertain, we surely
can't say what the digit after it is! So we use the addition
/ subtraction rule and round the answer to three decimal places.
164.037 g - 15.6423 g =
148.395 g sodium chloride
Rounding
In the two examples above, we rounded
answers to the correct number of significant digits. The rounding
rules we'll use in this class are the same as the ones you were
likely taught in grade school:
Don't round any numbers except the
result of your final calculation. This minimizes so-called
"roundoff error". In short, don't round until the end.
If the first insignificant digit
to be dropped is less than five, just drop the insignificant
digits - round down.
If the first insignificant digit
is five or greater, add 1 to the last significant digit and
then drop all the insignificant digits - round up.
Let's round pi off to different
numbers of significant figures. Pi has a value of 3.14159265...
(it goes on, and on, and on ...)
|
Significant figures
|
Rounded number
|
|
3
|
3.14
|
|
4
|
3.142
|
|
5
|
3.1416
|
|
6
|
3.14159
|
For 3 and 6 significant figures, we had
to round down. For 4 and 5 significant figures, we had to round up.
Exact numbers
Some numbers are exact ,
which means that they contain no
uncertainty . For example, a normal human has five fingers on
each hand. If you pull three paper clips out of a box, you're
certain that you got three - not four or two. Numbers found by
counting objects are exact, and we say that they have an
infinite number of significant digits.
Some other numbers are exact - like
many conversion factors for units. There are exactly 100 centimeters
in a meter, and exactly 12 inches in a foot. In a calculation, you'd
treat these conversion factors as if they have an infinite number of
significant figures.
Summary
In this note pack, we've discussed
accuracy and precision - their definitions and how they relate to
experiments performed in chemical laboratories. You should know that
you can get a feel for the accuracy and precision of your
measurements by comparing them with known standards and by performing
repeated measurements. We discussed that significant figures are a
way to indicate the precision of measurements and how to report the
correct number of significant figures for measurements you make in
the lab. You should also know how to determine by simply looking at
a number how many significant figures (and thus how precise) the
number is. You should also have learned the rules for math with
significant figures, rounding, and how to deal with exact numbers.
These concepts are important in chemistry because chemistry depends
on quantitative, reproducible measurements of chemical reactions.
You'll be required to keep track of your precision in most of the
labs we do in the course.
All original site content ©2007 Charles Taylor. Page updated: November 28, 2007.







